10271. ADA School
In the ADA School classroom, there
are n × m desks arranged in a rectangular grid with n
rows and m columns. Each desk is occupied by exactly one student.
Before the lesson begins, the teacher
decides to shuffle the students a bit. After the rearrangement, two conditions
must be met:
·
Each
desk must still be occupied by exactly one student.
·
Each
student must move to a desk adjacent to their original one, meaning a desk
located directly to the left, right, above, or below.
Is it possible to rearrange the students
while satisfying both conditions?
Input. The first line contains the number of test cases t.
Each of the next t lines contains two integers n and m (2 ≤ n, m ≤ 1000).
Output. For each test case, print “YES” if the rearrangement
is possible and “NO” otherwise.
|
Sample
input |
Sample
ouutput |
|
|
2 5 5 4 4 |
NO YES |
|
SOLUTION
mathematics
Algorithm analysis
Let’s consider the case where
one of the grid dimensions is even. For example, let n (the number of
rows) be even. In this case, the rearrangement of students can be performed as
follows:
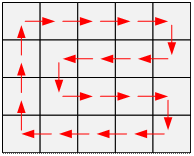
If n and m are both odd, the rearrangement is
impossible.
Consider a grid colored in a checkerboard pattern, where some
cells are white and others are black. When a desk is moved, it must switch from
a black cell to a white one, and vice versa. For the rearrangement to be
possible, the number of white and black cells must be equal. Therefore, the
total number of desks must be even.
However, when both n and m are odd, the total
number of desks, n × m, is an odd number, making the
rearrangement impossible.
Algorithm implementation
Read
the number of test cases t.
scanf("%d", &t);
while (t--)
{
Read
the input data for each test case.
scanf("%d %d", &n, &m);
If
n and m are both
odd, print “NO”.
if (n % 2 == 1
&& m % 2 == 1)
puts("NO");
Otherwise,
print “YES”.
else
puts("YES");
}